Tham khảo cách tính diện tích toàn phần và diện tích xung quanh hình lập phương mới nhất được Thptlequydontranyenyenbai.edu.vn tổng hợp chi tiết trong bài viết sau!
Hiện nay ngoài việc nghiên cứu về con số, Toán học cũng có một mảng kiến thức quan trọng là về hình học. Bạn có thể bắt gặp nhiều đồ vật dưới dạng hình vuông, tròn, chữ nhật trong đó cũng có thể có hình lập phương. Bài viết này Thptlequydontranyenyenbai.edu.vn sẽ tổng hợp cho bạn các thông tin về hình lập phương là gì? Cách tính diện tích toàn phần và diện tích xung quanh hình lập phương chi tiết dưới đây nhé.
1. Hình lập phương là gì?
Hình lập phương là hình khối có chiều rộng, dài, cao đều bằng nhau. Với 6 mặt đều là hình vuông và hình lập phương cũng là hình chữ nhật có tất cả các cạnh bằng nhau.
Tính chất của hình lập phương là: Có 8 mặt đối xứng, 12 cạnh bằng nhau, 8 đỉnh, 3 cạnh gặp nhau tại 1 điểm. Ngoài ra có 4 đường chéo cắt nhau tại 1 điểm còn gọi là tâm đối xứng của hình lập phương và đường chéo của hình khối lập phương là bằng nhau.
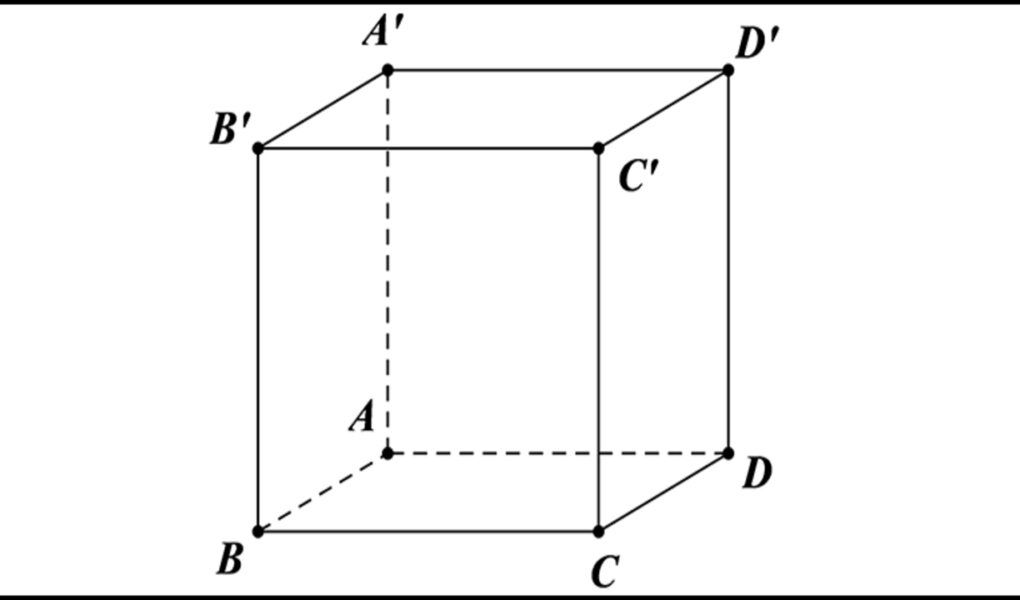
Quy ước:
- a: Độ dài của cạnh lập phương
- P: Chu vi hình lập phương
- S(bm): Diện tích bề mặt hình lập phương
- Sxq: Diện tích xung quanh hình lập phương
- S(tp): Diện tích toàn phần hình lập phương
- V: thể tích
2. Công thức tính diện tích toàn phần hình lập phương
Diện tích toàn phần của hình lập phương bằng diện tích một mặt nhân với 6.
Công thức: Stp = a x a x6
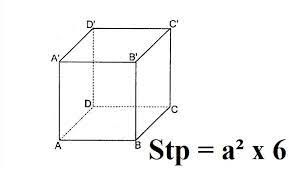
Ví dụ: Tính diện tích phần của hình lập phương có cạnh bằng 3
Đáp án: Diện tích toàn phần hình lập phương bằng: 3 x 3 x 6 =54 cm2
3. Công thức tính diện tích xung quanh hình lập phương
Diện tích xung quanh hình lập phương bằng diện tích một mặt nhân 4.
Công thức: Sxq = a x a x 4
Ví dụ: Tính diện tích xung quanh của hình lập phương có cạnh 8cm.
Đáp án: Diện tích xung quanh của hình lập phương là: 8 x 8 x 4 =256( Cm2)
4. Một số dạng bài tập tính diện tích hình lập phương
Dưới đây Thptlequydontranyenyenbai.edu.vn sẽ giới thiệu cho bạn một số dạng bài tập tính diện tích hình lập phương phổ biến nhất bạn có thể tham khảo và áp dụng vào trong quá trình học bộ môn Toán hình này nhé.
Bài 1: Cho hình lập phương B có diện tích toàn phần là 384 cm2, hỏi thể tích hình lập phương là bao nhiêu?

Đáp án:
Diện tích 1 mặt của hình lập phương B là: 384 : 6 = 64 cm2
Độ dài hình lập phương là 64: 8 = 8 cm
Thể tích lập phương B là: : 8x8x8= 5126cm3
Bài 2: Cho hình lập phương ABCDEF với lần lượt kích thước cạnh là 5cm. Tìm diện tích xung quanh và diện tích toàn phần của hình đó
Đáp án:
Diện tích xung quanh là 5 x5 x 5 = 125m2
Diện tích toàn phần ABCDEF là 5 x 5 x 6 = 150m2
Bài 3: Tính diện tích xung quanh và toàn phần của hình lập phương có cạnh là 11cm.
Đáp án:
Sxq= 11 x11 x4 = 484cm2
Stp= 11 x 11x 6=726cm2
Bài 4: Nếu làm 1 cái hộp bằng tôn không nắp có dạng lập phương với độ dài cạnh là 9cm. Vậy diện tích miếng tôn cần dùng để làm hộp bao nhiêu
Đáp án: Diện tích tôn cần dùng là 9 x 9 x 5 = 405cm2
Bài 5: Cho 2 hình vẽ sau được sắp xếp bởi các hình lập phương cạnh dài 10cm. Nếu sơn tất cả mặt ngoài của 2 hình. Tính diện tích sơn cần dùng mỗi hình.
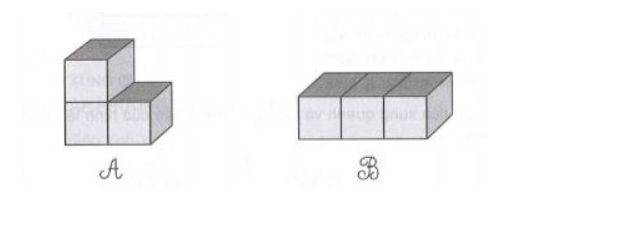
Đáp án:
Hình A là 1400cm2, Hình B là 1400cm2
Bài 6: Cho hình lập phương với diện tích toàn phần là 216cm2. Hỏi: Cách tính diện tích xung quanh và cạnh hình lập phương.
Đáp án:
Diện tích 1 mặt hình lập phương là 216:6= 36cm2 => Diện tích xung quanh là 36 x 4 = 144cm2
Độ dài cạnh lập phương: 36:6 = 6cm
Bài 7: Lan dán giấy màu vào các mặt của hộp quà lập phương với cạnh có độ dài 4 cm. Hỏi diện tích giấy đã dán là bao nhiêu
Đáp án: diện tích giấy Lan dán là 4 x 4 x 6= 96 cm2.
Bài 8: Sắp xếp 1 vài viên gạch thành hình lập phương với cạnh dài 15 cm. Hỏi diện tích xung quanh và toàn phần khối lập phương. Tính thêm kích thước viên gạch bao nhiêu.
Đáp án:
Diện tích Sxq= 15 x 15 x 4 = 900cm2
Diện tích toàn phần Stp= 15×15 x6= 1250cm2
Do là hình lập phương cạnh 15cm nên chiều dài = chiều rộng = chiều cao của viên gạch. Vì thế mà viên gạch có chiều dài là 15cm.
Hy vọng với chia sẻ về cách tính diện tích toàn phần và diện tích xung quanh hình lập phương ở trên sẽ giúp bạn hiểu rõ hơn về cách tính hình lập phương. Dựa vào đó kết hợp củng cố thêm các bài luyện tập để mang đến kiến thức và nhiều cách giải bổ ích cho mình. Đừng quên liên hệ Thptlequydontranyenyenbai.edu.vn để được hỗ trợ nhanh chóng nhé.

