Các công thức tính chu vi tam giác cần nắm rõ để áp dụng vào các bài tập. Từ đó có thể nhìn nhận tổng thể rõ ràng hơn.
Các công thức tính chu vi tam giác là kiến thức cơ bản cần thiết cho học sinh lớp 9. Để giải bài tập một cách nhanh nhất và hiểu vấn đề thì bạn cần nắm vững các công thức được chúng tôi tổng hợp ngay dưới đây.
1. Cách tính chu vi hình tam giác
Chu vi của một tam giác có nghĩa là tổng của cả ba cạnh. Từ chu vi là sự kết hợp của hai từ Hy Lạp – “peri” có nghĩa là xung quanh và “metron” có nghĩa là thước đo. Tổng khoảng cách xung quanh bất kỳ hình dạng 2D nào được định nghĩa là chu vi của nó. Vì chu vi cho biết độ dài của đường bao của một hình, nên nó được biểu thị bằng đơn vị tuyến tính.

Cách tính chu vi nhanh và dễ hiểu đối với hình tam giác
Ví dụ thực tế về chu vi của tam giác: Hãy tưởng tượng rằng chúng ta cần rào công viên hình tam giác được hiển thị bên dưới. Bây giờ, để có thể biết kích thước của hàng rào thì chúng ta sẽ cộng độ dài của ba cạnh của công viên lai với nhau. Kết quả này là chu vi của tam giác đó.
1.1 Công thức chu vi tam giác thường
Để tính chu vi của một tam giác, ta chỉ cần cộng độ dài các cạnh đã cho. Công thức cơ bản được sử dụng để tính chu vi của một tam giác là:
Chu vi = tổng ba cạnh
1.2 Công thức tính chu vi tam giác cân
Nếu một tam giác có độ dài hai cạnh bằng nhau thì đó là tam giác cân. Chu vi của một tam giác cân có thể được tính bằng cách tìm tổng của các cạnh bằng nhau và không bằng nhau. Công thức tính chu vi tam giác cân là: Chu vi tam giác cân = 2a+b đơn vị.
a = các cạnh có độ dài bằng nhau
b = cạnh thứ ba
1.3 Công thức tính chu vi tam giác đều
Một tam giác đều có tất cả các cạnh có số đo bằng nhau. Công thức sau đây giúp bạn tính chu vi của tam giác đều là:
Chu vi tam giác đều = (3 × a) đơn vị.
trong đó ‘a’ = độ dài mỗi cạnh của tam giác.
Tính chu vi tam giác cân như thế nào?
1.4 Công thức tính chu vi tam giác vuông
Tam giác có một trong các góc bằng 90° được gọi là tam giác vuông hoặc tam giác vuông. Chu vi của một tam giác vuông có thể được tính bằng cách cộng các cạnh đã cho. Công thức sau đây giúp bạn tính chu vi tam giác vuông là:
Chu vi tam giác vuông, P = a + b + c đơn vị.
Vì đây là một tam giác vuông, nên chúng ta có thể sử dụng định lý Pythagoras, nếu bất kỳ cạnh nào của tam giác này chưa được biết. Định lý Pythagoras đã chỉ ra rằng bình phương của cạnh huyền trong tam giác sẽ bằng tổng bình phương của hai cạnh góc vuông còn lại. Đề cập đến con số đưa ra ở trên:
a = Vuông góc
b = Cơ sở
c = Cạnh huyền
Do đó, theo định lý Pythagoras, c2 = a2 + b2. Trong trường hợp này, chu vi của một tam giác vuông cũng có thể được viết là: P = a + b + √(a2 + b2). Điều này là do c2 = a2 + b2 , do đó, c = √(a2 + b2).
1.5 Công thức tính chu vi tam giác vuông cân
Tam giác vuông có hai cạnh bằng nhau và hai góc bằng nhau được gọi là tam giác vuông cân. Chu vi của một tam giác vuông cân có thể được tính bằng cách cộng các cạnh đã cho.
Công thức tính chu vi của tam giác vuông cân là P = 2l + h, trong đó l là độ dài của hai cạnh góc vuông bằng nhau và h là cạnh huyền.
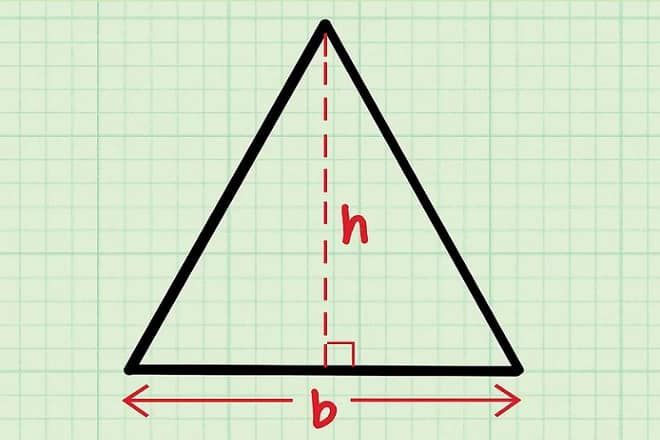
Đối với cách tính chu vi của tam giác vuông cân
Một điểm thú vị khác cần lưu ý ở đây là sử dụng định lý Pythagoras, chúng ta biết, h = √(l2 l2) = √2 × l hay, l = h/√2 đơn vị. Do đó, chu vi của một tam giác vuông cân cũng có thể được viết là: P = 2l (√2)l = (2 √2)l đơn vị.
Ngoài ra, P = 2(h/√2) h = (√2 × h) h đơn vị.
2. Hướng dẫn 1 số dạng bài tập tính chu vi hình tam giác
Chu vi của một tam giác có thể được tính bằng cách làm theo các bước được đưa ra dưới đây:
Bước 1: Tính chu vi tam giác, số đo các cạnh đã cho
Muốn tính chu vi tam giác ta tính độ dài ba cạnh của tam giác
Bước 2: Tính chu vi hình tứ giác khi biết độ dài các cạnh
Để tính chu vi tứ giác ta tính tổng các cạnh của tứ giác.
Bước 3: So sánh độ dài một đoạn thẳng và chu vi của một tam giác, tứ giác Biết số đo các đoạn thẳng
- Đặt lại cùng một vị trí
- Tính tổng chiều dài của đoạn gấp khúc bằng cách cộng số đo của các đoạn thẳng với nhau rồi so sánh với chu vi của hình.
Ví dụ: Tìm chu vi của △ABC có các kích thước sau: AB = 6 cm, BC = 8 cm, AC = 10 cm.
Giải:
Bước 1: Kiểm tra xem đã biết cả ba cạnh của tam giác chưa.
AB = 6 cm, BC = 8 cm và AC = 10 cm
Bước 2: Sử dụng công thức thích hợp và cộng các cạnh để được chu vi. Vì đây là một tam giác cân, nên chúng ta sử dụng công thức, Chu vi = a + b + c. Viết chu vi cùng với các đơn vị của nó.
Chu vi tam giác ABC = 6 + 8 + 10 = 24 cm.
3. Các ví dụ đã giải về công thức Chu vi Tam giác
Ví dụ 1: Tìm chu vi tam giác có các cạnh lần lượt là 3 cm, 5 cm và 7 cm
Trả lời:
Theo công thức thì P= a + b + c,
Do đó, P = 3 + 5 + 7 = 15 cm.
Ví dụ 2: Nếu P = 30cm và a = 5 và b = 7 thì c là bao nhiêu?
Trả lời:
Sử dụng công thức P = a + b + c, thay mọi thứ đã cho vào công thức
Những thứ đã cho là P=30, a=8 và b = 10
Thay thế chúng vào công thức sẽ cho:
30 = 8+ 10+ c
30 = 18 + c
Do đó, c = 12.
Ví dụ 3: Tìm độ dài hai cạnh bằng nhau của một tam giác cân biết độ dài cạnh không bằng nhau là 5cm và chu vi là 17cm.
Giải:
Biết độ dài cạnh không bằng nhau là 5cm, chu vi là 17cm.
Vì là tam giác cân nên độ dài hai cạnh còn lại bằng nhau. Đặt độ dài mỗi cạnh bằng nhau là đơn vị ‘a’.
Do đó, chu vi = a + a + 5
Vì, chu vi = 17cm, chúng ta có thể viết,
17 = 2a + 5
2a + 5 = 17
2a = 12
a = 6cm
Vậy độ dài các cạnh bằng nhau của tam giác cân là 6cm.
Ví dụ 4: Cho chu vi tam giác đều là 21cm, tìm độ dài ba cạnh của tam giác đó.
Giải:
Vì trong tam giác đều, ba cạnh có độ dài bằng nhau nên chu vi bằng ba lần độ dài một cạnh.
Gọi độ dài của một cạnh bất kỳ bằng đơn vị ‘a’. Vậy chu vi bằng ‘3a’ đơn vị.
Vì vậy, chúng ta có thể viết,
3a = 21
a = 7cm
Như vậy độ dài mỗi cạnh bằng 7cm.
Một số bài tập dành cho bạn tự luyện tại nhà:
Câu 1: Hãy tìm chu vi hình tam giác ABC biết tam giác có độ dài các cạnh lần lượt là: 27cm, 3dm và 22cm.
Câu 2: Cho tam giác MNP có ba cạnh đều bằng nhau, cạnh MN = 5dm. Tìm chu vi tam giác MNP.
Câu 3: Cho tam giác EFJ có độ dài cạnh EF bằng 12cm.Tổng độ dài hai cạnh FJ và JE hơn độ dài cạnh EF là 7cm.
a. Tìm tổng độ dài hai cạnh FJ và JE
b. Tìm chu vi tam giác EFJ.
Câu 4: Tam giác OPQ có ba cạnh bằng nhau và có chu vi bằng 84dm. Hỏi cạnh OP dài bao nhiêu đề-xi-mét?
Trên đây là các thông tin tổng quan được chúng tôi tổng hợp lại về chu vi tam giác cũng như hướng dẫn giải chi tiết một số bài tập liên quan tương ứng. Hy vọng rằng qua những thông tin hữu ích trên có thể giúp bạn trong quá trình học và làm bài của bạn.

